Die Mobilität der Zukunft
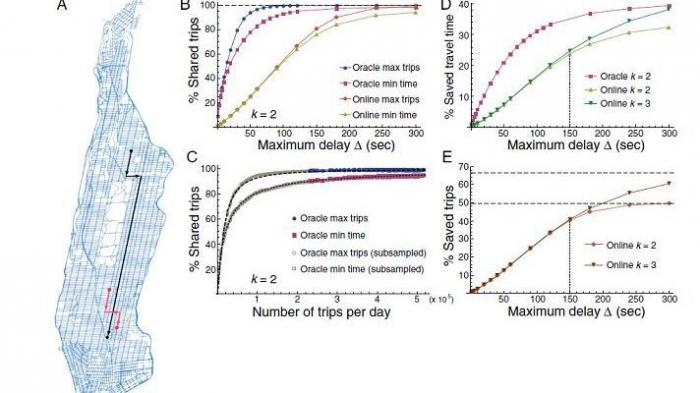
Abb. 1: Die Karte von Manhattan (A) und die Ersparnisse bei Taxifahrten mit zwei bzw. drei passagiere (k=2 bzw k=3). Ein Orakel kann mit voller Übersicht der Zukunft die Fahrten optimieren, oder die Entscheidung über die abzuholende Passagiere kann in Echtzeit getroffen werden (Santi et al. 2014).
- Die Mobilität der Zukunft
- Helsinki und das Ende des Automobils
- Die optimale Zuordnung
- Auf einer Seite lesen
Eine Ökonomie des Teilens?
Langsam durchdringt die "sharing economy" auch die Welt des Automobils. Mehr und mehr Unternehmen führen verschiedene Arten von Mitfahrgelegenheiten ein, die zwischen Privatpersonen vermitteln oder Kunden an Taxifahrer weiterleiten. Eine neue Studie zeigt, dass in New York ein Großteil der Taxis überflüssig wäre, wenn sich die Kunden die Taxis mit zusätzlichen Passagieren teilen würden.
Wahrscheinlich hatten die anspruchsvollen Proceedings of the National Academy of Sciences sich noch nie mit dem faden Problem der Mitfahrgelegenheiten beschäftigt. Vor kurzem wurde jedoch ein Beitrag veröffentlicht, der anhand von echten Daten zeigt, dass in New York bis zu 40% der von Taxis gefahrenen Kilometer eingespart werden könnten.1 Die Autoren, eine Gruppe von Italienern und Amerikanern, haben die Fahrdaten der 13.586 in New York registrierten Taxis erhalten und ausgewertet (immerhin 150 Millionen Fahrten, für das Jahr 2011).
Sie haben versucht, a posteriori, mehr als eine Person in jedem Taxi unterzubringen, unter der Annahme, dass die Passagiere bereit wären, das Taxi zu teilen. Wenn die Passagiere bis zu maximal 5 Minuten zusätzliche Warte- bzw. Fahrtzeit hinnehmen würden, ließen sich fast die Hälfte der Fahrten sparen (bei einer Durchschnittsbelegung von zwei Passagieren pro Taxi), wobei jede Fahrt notwendigerweise etwas länger wird.
Das mit der Studie angesprochene "car-pooling" hat in den USA seit den siebziger Jahren eine gewisse Tradition. Damals ist der Erdölpreis enorm gestiegen und dies hat zu den ersten "car sharing"-Ansätzen geführt. Die chronische Überfüllung der Autobahnen hat außerdem eine für Fahrgemeinschaften reservierte Spur entstehen lassen, auf der nur Autos mit zwei oder mehr Insassen fahren dürfen. Das sollte den Autofahrern einen Anreiz geben, Mitfahrgelegenheiten zu organisieren.
Dies geschieht heute sogar in manchen Städten auf spontane Art und Weise: Bereitwillige Fahrer stellen sich an verschiedene Stationen (häufig neben Parkplätzen) und nehmen Passagiere mit. So spart der Autofahrer Zeit, weil er oder sie auf der schnelleren Car-pooling-Spur fahren darf, und die Mitfahrenden sparen Nerven, weil sie nicht selbst fahren müssen. Bei organisierten Fahrgemeinschaften können sich Fahrer und Passagiere durch ein System von Punkten abwechseln. Jeder ist ab und zu als Fahrzeugführer dran.
Der Ansatz der Autoren der Studie über die Taxis in New York war relativ einfach: Sie haben von den 150 Millionen Fahrten im Jahr 2011 diejenigen ermittelt, die sich zeitlich und räumlich partiell überlappen. Für je zwei passende Fahrten haben sie dann ein Taxi statt zwei genommen, und die Fahrtroute dementsprechend angepasst. Die zusätzliche Wartezeit für den zweiten Passagier wurde zwischen 0 und 300 Sekunden eingegrenzt.
Für die Simulation der Fahrzeit über die neue Route wurden statistische Verkehrsdaten und das Straßennetz verwendet. Abb. 1 zeigt die wesentlichen Ergebnisse: bei zwei Passagieren pro Taxi (k=2) steigt die Anzahl der gemeinsamen Fahrten fast bis zu 100% bei einer maximalen Verzögerung von 300 Sekunden. Es werden zwei Arten von Taxibelegungen verglichen: Wenn alle Daten des Tages bekannt sind, kann man die beste Fahrstrategie berechnen (ein allwissendes "Orakel" kennt alle diese Daten). Da dies unrealistisch ist, wird auch geprüft, wie gut die Taxi-Belegung sein kann, wenn die Entscheidung, welches Taxi welchen Passagier abholt, in Echtzeit getroffen wird (d.h. online). Man kann bei der Berechnung die Anzahl der Fahrgemeinschaften maximieren (max trips) oder die Zeit für die Passagiere minimieren (min time).
Die Grafik links in Abb. 1 (B) zeigt die entsprechenden Resultate. Die Echtzeitbelegung, die realistischere Annahme, benötigt etwa 300 Sekunden zusätzliche Fahrzeit um die Sättigung zu erreichen. Die Grafik rechts in Abb. 1 (D), zeigt die Ergebnisse für zwei und drei Passagiere (k=2 bzw. k=3). Bei drei Passagieren kann man deutlich Fahrzeit sparen, auch ohne Orakel.
Die Idee ist recht einfach, wie man sieht, nur die Details sind etwas komplizierter. Würde man in Echtzeit Fahrgemeinschaften mit den Taxis bilden, müssten alle Taxis ihre Position einer Verkehrszentrale melden. Dies geschieht bereits in einigen Städten, aber nicht überall. Dann müssten die Profile der Passagiere und ihre Wünsche verwaltet werden. Wer es sehr eilig hat oder wer grundsätzlich allein fahren will, kann so ein Taxi bestellen.
Frauen könnten angeben, sie möchten nur mit anderen Frauen fahren. Raucher könnten ein Rauchertaxi bestellen (falls es so etwas gibt), usw. D.h. die Kunden setzen eine Reihe von "constraints" für den Taxidienst und es ist Aufgabe der Software, all diese Randbedingungen zu erfüllen. Außerdem sollten alle Passagiere über ein Mobiltelefon verfügen, um ihre Position zu erhalten und die Fahrt am Ende elektronisch, mit Preis je nach Belegung des Taxis, abzurechnen.
Alles lösbar, aber nicht in polynomieller Zeit: Solche kombinatorischen Aufgaben mit Randbedingungen ufern sehr schnell aus - die Rechenzeit kann exponentiell steigen. Es gibt allerdings Heuristiken und stochastische Verfahren, die auch in solchen Situationen helfen können. Die optimale Lösung wird damit nicht erreicht, aber doch ein guter brauchbarer Kompromiss.
Fahrten für Taxikunden zu organisieren ist ein Problem der Mischung von Trajektorien in Graphen. Die Uhrzeit der Taxibestellung ist wichtig, ebenso wie die benötigte Trajektorie, je nach Anfangs- und Endpunkt der Fahrt. Abb. 2 zeigt ein Beispiel der Fusion der Fahrten von sieben Passagieren, die von drei Taxis bedient werden können. Santi et al. nennen ihren Ansatz "Netzwerkfusion". Es wird zuerst für alle Passagiere (die Knoten im Lösungsgraphen) geschaut, welche Fahrten von zwei Knoten kompatibel sein könnten [brbr1](je nach Trajektorie und Uhrzeit).
Bei der Berechnung werden Paare von Knoten gebildet, deren Fahrten kompatibel sind und eine Kostenfunktion minimieren. Einige Knoten können alleine bleiben (z.B. T7 im Bild). Forscher aus der theoretischen Informatik, die Graphen über alles lieben, haben hier ein neues Einsatzgebiet.
