Die Kosmische Inflation und die Suche nach Raum-Zeit-Fossilien
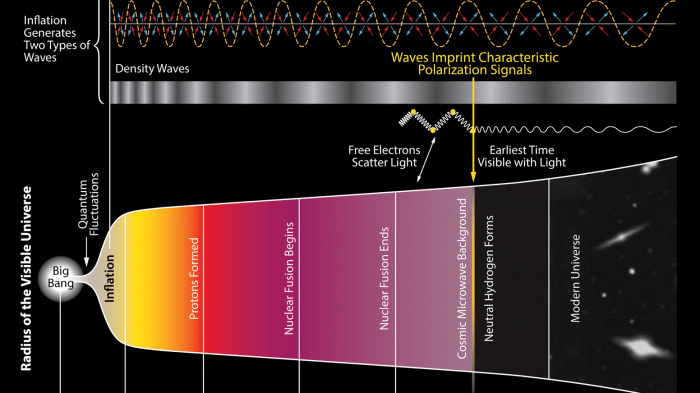
Bild: Einweichen/CC BY-SA-3.0
Als Kosmische Inflation bezeichnet man die Ära, in der das Universum seinen Durchmesser in Bruchteilen einer Sekunde circa hundertmal nacheinander verdoppelte. In den letzten Jahren ist über Alternativen diskutiert worden
Die Kosmologen haben heute ein sehr gutes theoretisches Verständnis der Entwicklung des Universums ab einer Sekunde nach dem Urknall. Sogar bereits nach nur einer Mikrosekunde (Quark-Ära) passt das Standardmodell der Teilchenphysik sehr gut zu den berechneten Temperaturen und Energien des frühen Universums.
Ab der Quark-Ära, bei der ein sogenanntes Quark-Gluon-Plasma das Universum ausgefüllt hat, haben drei der vier Elementarteilchen-Interaktionen angefangen, sich voneinander zu trennen (d.h. schwache Wechselwirkung, starke Wechselwirkung und Elektromagnetismus) und die Physiker können die Weiterentwicklung des Universums mit dem Standardmodell und mit Einsteins Gravitationstheorie verfolgen. Viel spekulativer sind dagegen diverse Phasen vor der Quark-Ära, insbesondere die Periode der sogenannten Inflation des Universums.
Gab es etwas vor dem Urknall? Es gibt mehrere mögliche Antworten auf diese Frage. Die erste wäre die sehr pragmatische Entgegnung von Stephen Hawking. Der Cambridge-Physiker meinte, dass Ereignisse vor dem Urknall von uns heute nicht mehr beobachtet werden können und wir deswegen getrost unsere Uhren ab da starten dürfen. Anders gesagt: Es gibt von dem "Vor-Urknall" keine Strahlungs- bzw. Teilchen-Rückstände, die wir untersuchen bzw. messen könnten. Kognitiv gesehen ist diese Zeit vor dem Urknall nicht erfassbar und für uns deswegen unerheblich.
Theoretiker wie Paul Steinhardt haben eine alternative Theorie vorgeschlagen, nämlich die sogenannte Rückprall-Kosmologie (bouncing cosmology), die ein oszillierendes Universum postuliert, das sich von einem Big-Bang zum nächsten weiterentwickelt. Nach Steinhardt verdünnt sich das Universum durch Expansion (über Milliarden von Jahren), um dann jedes Mal von neuem mit einem frischen Big-Bang zu starten. Steinhardt glaubt, dass eventuell durch Messungen der Rückstände der Gravitationswellen beim Urknall in Zukunft entschieden werden kann, wer Recht hat, d.h. die Inflations- bzw. die Rückpralltheoretiker.
Der berühmte Sir Roger Penrose hat ein analoges oszillierendes Universum vorgeschlagen, das sich immer weiter ausdehnt und schließlich dem Kältetod erliegt. Schwarze Löcher fressen sich durch den Kosmos und machen ihn entsetzlich leer und uniform. Dann kollabiert das gesamte Universum wieder auf ein kleines Volumen und ein neuer Urknall ist die Folge. Im Unterschied zu Penrose schlägt aber Steinhardt keinen vorherigen Kollaps des Universums, sondern einfach einen periodischen Urknall vor, der das tote und kalte Universum wieder mit Energie und Gravitation ausfüllt.1
Penrose glaubt sogar, die Signatur des letzten Rückpralls in der kosmischen Hintergrundstrahlung sichtbar machen zu können (Abb. 1). Zusammen mit dem Armenier Vahe Gurzadyan hat er entdeckt, dass in der kosmischen Hintergrundstrahlung Muster aus konzentrischen Ringen zu finden sind. Dafür haben sie mehrjährige Messungen des WMAP-Satelliten und aus anderen Experimenten genommen und die Variabilität (die Varianz) der Temperatur der Hintergrundstrahlung berechnet. Sie finden in der Strahlung konzentrische Ringe mit niedriger Varianz. Diese deuten beide Physiker als Hinterbleibsel der Gravitationswellen der Kollisionen von schwarzen Löchern beim Prozess des Kollapses des Vor-Universums.2
So eine wegweisende Ankündigung ist natürlich von anderen Physikern sofort auf die Probe gestellt worden und es hat sich offenbar ergeben, dass die spezielle Mischung der Frequenzen in der Hintergrundstrahlung solche Muster spontan und zufällig erzeugen kann, sodass die Muster selbst keine Boten aus einem früheren Universum sind. Sie stellen Strukturen dar, die rein rechnerisch entstehen können.3
Trotzdem ist die Idee von Penrose in der heutigen Hintergrundstrahlung nach Effekten zu suchen, die uns vielleicht Einblick in die ersten Mikrosekunden nach dem Urknall und sogar davor, ein Beispiel dafür, wie man physikalische Theorien auf die Probe stellen kann. In der Kosmologie redet man über Zeiträume, die jenseits der menschlichen Erfahrung liegen. Obwohl wir am Himmel die Geschichte des Universums ab der Rekombination mit Teleskopen beobachten können (d.h. ab 380.000 Jahren nach dem Urknall), verdeckt die Hintergrundstrahlung selbst wie ein Vorhang alles, was vor der Rekombination geschehen ist.
Der Neutrino-Hintergrund, erzeugt eine Sekunde nach dem Urknall, wäre dafür sehr aussagekräftig. Da aber Neutrinos mit anderen Teilchen kaum wechselwirken, ist es unheimlich schwer, sie zu detektieren. Die Physiker sind schon froh, wenn sie in riesigen Detektoren unter einem Berg eine Handvoll hochenergetische Neutrinos aus der Sonne ergattern können. Die Frage ist aber, ob es nicht andere physikalische Fossilien gibt, die uns hinter den Schleier der Rekombination blicken lassen. Beste Kandidaten sind z.Zt. die Gravitationswellen, die beim Urknall erzeugt wurden (oder sogar davor wie bei Penrose).
Wir denken normalerweise nicht so, aber eigentlich ist die Proportion zwischen Wasserstoff und Helium im Universum ein solches Fossil der Raum-Zeit-Geschichte. George Gamow hat als Erster das frühe Universum als chemische Retorte modelliert und zusammen mit Alpher die Proportion der leichten Elemente im Universum anhand der Urknall-Theorie zum ersten Mal erklären können. Noch ein mögliches Fossil ist die Polarisation der Photonen in der Hintergrundstrahlung. Physiker werden sicherlich nach weiteren Nachweismethoden Ausschau halten, um die vorgeschlagenen Theorien auf sichere experimentelle Basis stellen zu können. So gesehen, sind Kosmologen heute so etwas wie Paleo-Astronomen, Fossilienjäger also.
Das inflationäre Universum
Die Inflations-Theorie des Universums wurde von Alan Guth Anfang der Achtzigerjahre vorgeschlagen. Die Zusammenfassung davon ist einfach, die Erklärung etwas aufwendiger, und die Darstellung der heutigen Paradoxien viel komplexer.
Fangen wir mit der Zusammenfassung an: Fast gleich nach dem Urknall hat das Universum eine Periode der ultraschnellen Expansion erlebt. Vor der Inflation war das Universum viel kleiner als ein Proton. Dann erlebte das Universum in einer erstaunlich kurzen Zeit circa 100 Größenverdoppelungen nacheinander. Am Ende der Inflationsperiode war das Universum etwa so groß wie ein Apfel. Ab dann ging es "normal" mit der von der sogenannten Friedmann-Gleichung vorhersagten langsameren (aber doch schnellen) Expansion des Universums weiter (Abb. 2).
Die ursprüngliche Motivation von Alan Guth war, die Bedingungen für Vereinheitlichungstheorien (grand unified theories) der Naturkräfte zu untersuchen. Eine solche Vereinheitlichung geschieht nur bei ultrahohen Temperaturen und Energiekonzentrationen. Man muss sich also zum Zeitpunkt der Geburt des Universums zurückversetzen, um solche Bedingungen vorfinden zu können. Guth fand aber mehr als er suchte, als er eine Art von Vakuumenergie postulierte, die sich als "Skalarfeld" verhält. Das ist eine Art von Energie deren Dichte konstant bleibt, auch wenn das Universum sich vergrößert. Wenn sich hingegen ein Gas in einem Kubikmeter Volumen auf zehn Kubikmeter verteilt, verdünnt sich die Materiedichte um den Faktor 10.
Aber Vakuum bleibt Vakuum, und wenn sich das Vakuum um den Faktor 10 vergrößert, steigt die Vakuumsenergie auch um den Faktor 10. Gleichzeitig wird aber ein Gravitationsfeld erzeugt. Das Gravitationspotential ist aber negativ, d.h. die schnelle Vergrößerung der Größe des Universums ist das ultimative "free lunch" (wie Guth sagt). Die positive Energie, die im Skalarfeld im Vakuum größer wird, gleicht sich mit der negativen Energie des entstandenen Gravitationsfeldes aus. Wenn der Ausgleich perfekt ist, wird erstens der Energieerhaltungssatz nicht verletzt und zweitens wird das Universum "flach".
Guth wusste es nicht, aber er hatte eine ähnliche Lösung gefunden wie Willem de Sitter im Jahr 1917, als er ein Universum ohne Materie mit Hilfe der Einstein-Gleichung untersuchte. Implizit setzte er eine positive kosmologische Konstante in die Gleichungen ein, was wir heute als "dunkle Energie" bezeichnen würden. De Sitter kam zu der Schlussfolgerung, dass ein solches Universum sich exponentiell ausdehnen sollte. Da de Sitters Universum aber keine Materie enthielt, schien es eine Art reine Rechenübung zu sein. In einem de-Sitter-Universum mit einer positiven kosmologischen Konstante ist die Ableitung des Skalierungsparameters der Größe des Universums gleich jener Konstante mal dem Skalierungsparameter (also a = Λa), d.h. eine Gleichung, die die Lösung a = eΛt besitzt. Und das ist exponentielles Wachstum. Ist Λ sehr groß und dominiert alle anderen Parameter, ergibt sich eine ultraschnelle Expansion.
Abb. 3 zeigt Guths Vorschlag. In einer sehr kurzen Zeit ist das Universum (Milliarden mal kleiner als ein Proton) bis in den Bereich von Zentimeter-Durchmesser angewachsen. Abb. 3 benutzt einen logarithmischen Maßstab, sodass die Wachstumsgeraden in der Abbildung exponentiellem Wachstum entsprechen. Während der Inflation hat sich das beobachtbare Universum mehr als um den Faktor zwei stärker ausgedehnt als in den 13,7 Milliarden Jahren danach.
Die physikalische Erklärung von Guth für das Inflations-Phänomen war, dass das frühe Universum in ein sogenanntes falsches Vakuum startete, d.h. das Vakuum besaß nicht das absolut mögliche Minimum an Energie. Solange das falsche Vakuum besteht, drückt das Skalarfeld nach außen (negativer Druck) und vergrößert auf diese Weise den Raum, so wie die Lösung von de Sitter es vorsieht. Dieser Zustand kann aber nicht für immer aufrechterhalten werden. Das Skalarfeld "rollt" eventuell ins Energieminimum und die Expansion des Raumes aus dieser Quelle hört auf. Die im Feld gespeicherte Energie zerfällt dann in übliche Materie und Energie und der "Knall" im Urknall ist damit abgeschlossen. Ab dann evolviert das Universum nach demselben Muster wie heute.
So kontraintuitiv und absonderlich diese Darstellung klingt, fand der Vorschlag von Guth ein großes Echo bei den Kosmologen, weil die Inflations-Theorie drei Probleme mit einem einzigen Mechanismus lösen konnte. Diese Probleme waren:
- Das Horizont-Problem
- Die Flachheit des Universums
- Das Ausbleiben von magnetischen Monopolen
Das letzte Problem ist am einfachsten zu erläutern. Nach den grand unified theories könnte man in den Gleichungen des Elektromagnetismus volle Symmetrie herstellen, wenn nicht nur die elektrischen Ladungen, sondern auch die magnetischen Pole ebenfalls einzeln vorgefunden werden könnten. Dann wären elektrische und magnetische Ladungen duale und symmetrische Eigenschaften von Elementarteilchen. Das experimentelle Problem ist jedoch, dass die Physiker trotz aller Anstrengungen die postulierten Monopole bis heute nicht finden können. Da eine Periode der Inflation jegliche vorexistierenden Teilchen unfassbar weit auseinander streut, wäre es kein Wunder, dass man sie nicht mehr finden kann. Im ganzen Solarsystem sollte es weniger als ein solches Ur-Monopol geben.
Das Horizont-Problem bedeutet folgendes: Die kosmische Hintergrundstrahlung zeigt, dass das Universum sich 380.000 Jahre nach dem Urknall im thermischen Gleichgewicht befand. D.h. die Temperatur ist dieselbe in jede Richtung, die man messen kann. Da aber das Licht wegen dessen endlicher Geschwindigkeit sich nicht von einer Seite des Universums bis zur anderen in der zuvor vorhandenen Zeit ausbreiten konnte (siehe Abb. 4), war das frühe Universum in vielen Inseln von "Kausalität" zerteilt (das sind die kleinen Kreise in der Abbildung). Bei jeder Insel konnte thermisches Gleichgewicht entstehen, aber nicht zwischen Inseln, die sehr weit auseinanderlagen. Wenn aber das Universum viel kleiner wäre, hätte thermisches Gleichgewicht hergestellt werden können, d.h. in einem ultrakleinen Universum gibt es überall eine kausale Verbindung. Die darauffolgende Inflation startet das danach vergrößerte Universum im thermischen Gleichgewicht.
Das Problem der Flachheit des Universums hat mit der kritischen Energiedichte zu tun. Heute glauben Astronomen, dass die Summe der Energie von Materie, dunkler Materie und dunkler Energie genau die sogenannte kritische Energiedichte ergibt. Die kritische Energiedichte ist jene, die das Universum euklidisch macht. In einem euklidischen Universum fliegen zwei Photonen, die auf Parallelbahnen geschossen wurden, für immer parallel. Weder kommen sie sich näher, noch entfernen sie sich mehr voneinander. Das Verhältnis zwischen gemessener und kritischer Energiedichte wird mit Ω dargestellt. In einem euklidischem Universum ist Ω=1.
Es ist jedoch so, dass die Gleichungen für die zeitliche Evolution von Ω jede Abweichung von Eins sehr schnell bestrafen. Wäre Ω am Anfang des Universums etwa 1,02 gewesen, hätten wir nach weniger Zeit Ω=2 gehabt. Das heutige Universum musste dann eine hohe Raumkrümmung aufweisen, eine, die wir nicht beobachten. Da die heutigen Messungen einen Wert für Ω sehr nah an 1,0 ergeben, ist das Universum perfekt bzw. fast perfekt mit Ω=1 gestartet, und zwar auf fünfzehn Dezimalzahlen genau. Die Inflationstheorie von Guth ergibt das gewünschte Ω=1, weil das Gravitationsfeld die erzeugte Energie perfekt ausgleicht und beide Bestandteile jede anderen Rückstände an Vor-Energie dominieren. Die Vor-Energie des Universums entspricht nur 25 Gramm an Materie - nach der Inflation jedoch Abermilliarden von Sonnenmassen.
Die notwendigen Gleichungen für alle diese Schätzungen können wir hier nicht behandeln, aber im Laufe der Zeit haben die Inflationstheoretiker sie vorgelegt und die Anzahl der Verdopplungen des Durchmessers des Universums bei der Inflation immer wieder neu berechnet. Das genauere Ergebnis hängt aber von den Anfangsbedingungen ab und hier hat sich eine Spaltung ergeben, sodass wir heute nicht eine Inflationstheorie, sondern eher eine Familie von Theorien haben (mehr als hundert, je nachdem, wie man sie gruppiert).
Paradoxon der ewigen Inflation: Die Kritik von Steinhardt
Paul Steinhardt ist heute nicht mehr mit der Inflationstheorie einverstanden, obwohl er am Anfang wesentliche Beiträge für seine Durchsetzung geliefert hat (und sogar den Dirac-Preis dafür bekommen hat). Heute hat er eine eigene Theorie (bouncing cosmology) und übt konstante Kritik an der Inflationstheorie.
Steinhardts Hauptproblem ist das sogenannte "graceful exit" aus der Inflation. Abb. 5 zeigt ein Modell für das langsame Abrollen des Skalarfeldes entlang eines Potentials bis zum Minimum. Beim "Wiederaufheizen" zerfällt die Energie des Skalarfeldes in Materie und übliche Energie und das durch die Inflation entleertes Universum füllt sich wieder. Nun hängt die genaue Entwicklung der Inflationsperiode von der Form dieses Potentials ab (das keiner kennt) und so sind diverse Potentialprofile vorgeschlagen worden. Jedes davon ändert die Details der Inflationsperiode. Deswegen gibt es so viele Inflationstheorien, viele davon unterscheiden sich nur im gewählten Potential.
Aber etwas Wichtigeres stört Steinhardt: Das Ende der Inflation ist ein quantenmechanisches Phänomen und ist deswegen stochastisch. Die Inflation kann an einer Stelle im Universum aufhören, aber wenn benachbarte Stellen weiter expandieren, dominieren die weiter expandierenden Teile das gesamte Universum sehr schnell. Das wird "ewige Expansion" genannt und ist ein echtes Problem in der Theorie (obwohl Guth eher daraus ein Feature der Theorie macht).
Ein Ausweg aus dem Paradoxon der ewigen Inflation besteht darin, unsere eigene Raum-Zeit-Blase, wo die Expansion aufgehört hat, als unser Universum zu deklarieren. Andere Blasen entwickeln sich zu Paralleluniversen, bei denen womöglich Naturkonstanten sogar andere Werte besitzen. Das ist die Idee des fraktalen "Multiversums", das von Andrei Linde popularisiert worden ist. Wir leben dann in einem Universum, in dem sich Leben und Kognition entfalten können (das anthropische Prinzip), es gäbe aber viele andere Universen, in denen sich vielleicht keine Galaxien und Planeten bilden können, weil es beispielsweise dort viel oder zu wenig an dunkler Materie gibt.
Auch in der Quantentheorie gibt es die Viel-Welten-Theorie, die Paralleluniversen immer dann postuliert, wenn ein Quanteneffekt zwei unterschiedliche Resultate liefern kann. Stephen Hawking hat solche Theorien als sehr sparsam bei den notwendigen Anfangsbedingungen aber sehr teuer an Universen bezeichnet. Eine ähnliche Haltung legt Steinhardt an den Tag: Es kann nicht sein, dass wir schon heute darauf verzichten die Naturkonstanten jemals zu berechnen und verstehen zu können, wenn ihre Werte nur ein zufälliges Ergebnis in unserem Universum sind und wir die anderen Universen sowieso nicht beobachten können.
Steinhardts Vorschlag ist allerdings nicht weniger einfallsreich. Er modelliert das Universum mit Hilfe von "Membranen", die aus der String-Theorie abgeleitet wurden. In der Stringheorie gibt es zusätzliche Dimensionen des Universums, die für uns nicht direkt wahrnehmbar sind. Unser Universum ist ein solches "brane" (aus Membrane), das periodisch mit einem anderen Universum (einem anderen brane) kollidiert. Jede Kollision ist wie ein Urknall, aber nicht lokal bei einer Singularität, sondern ein globaler Urknall, sodass das Horizontproblem nicht entstehen kann. Auch die Monopole würden sich in einem solchen Szenario nicht bilden und die Flachheit des Universums wäre durch den Mechanismus der Kollision garantiert.4
Steinhardt hat viel Kritik mit seinem Vorschlag aus der Ecke der Inflationstheoretiker erfahren, aber man muss doch zugeben, dass er nur noch zwei und nicht viele Universen braucht. Sabine Hossenfelder hat schließlich den Inflationstheoretikern die Leviten gelesen. Sie sagt, vielleicht gibt es einfach keine magnetischen Monopole, die Anfangsbedingungen des Universums waren einfach Ω=1 gewesen, und thermisches Gleichgewicht am Anfang der Zeit wäre ebenfalls denkbar.
Was sie jedoch außer Acht lässt, ist, dass die Existenz von magnetischen Monopolen die Quantisierung von Ladungen theoretisch erklärt und dass Ω=1 eine sehr feine Abstimmung der gesamten Masse des Universums mit dessen Expansion voraussetzt. Die Debatte ist jedenfalls nicht abgeschlossen und die Inflationstheoretiker bzw. die Kritiker werden sich noch sehr bemühen müssen, bis eine zufriedenstellende Theorie abgeschlossen werden kann.
Aber warum interessiert es uns überhaupt, was eine Mikrosekunde nach dem Urknall war, wenn wir die restlichen 13,7 Milliarden Jahren mehr oder weniger erklären und einen großen Teil davon sogar sehen können? Man könnte sagen, "because it's there", wie der Mount Everest. Aber eine bessere Erklärung wäre Hilberts Diktum, das auf die Mathematik bezogen lautet: "Wir müssen wissen, wir werden wissen."
Dass sich die Wissenschaftler auf dem Weg dahin manchmal verirren und Epizykeln und weitere Epizykeln in nicht ganz korrekte Theorien einbauen, ist nicht zu beklagen - viel schlimmer wäre es, es erst gar nicht zu versuchen.
Empfohlener redaktioneller Inhalt
Mit Ihrer Zustimmmung wird hier eine externe Buchempfehlung (Amazon Affiliates) geladen.
Ich bin damit einverstanden, dass mir externe Inhalte angezeigt werden. Damit können personenbezogene Daten an Drittplattformen (Amazon Affiliates) übermittelt werden. Mehr dazu in unserer Datenschutzerklärung.
